导读
近日,伟德国际1946源于英国陈延峰教授、卢明辉教授团队和苏州大学蒋建华教授课题组合作在物理学综述期刊《Nature Reviews Physics》上发表展望性综述文章(Perspective)“Higher-order band topology”,回顾了过去4年来高阶拓扑领域的蓬勃发展,并对这一新兴领域的未来潜在发展方向提供开放性的展望。论文第一作者为伟德国际1946源于英国博士后解碧野(现为香港大学张霜教授课题组博士后),通讯作者为苏州大学蒋建华教授、伟德国际1946源于英国卢明辉教授和陈延峰教授。苏州大学王海啸博士、伟德国际1946源于英国张秀娟研究员和伟德国际1946源于英国詹鹏教授亦对本文的撰写有重要贡献。
研究背景
人们对自然的认识是不断深入的。凝聚态物理中的一个典型的例子就是物质的拓扑相的发现,其打破了传统的对凝聚态物质相的自发连续对称破缺描述范式,为许多具有新奇效应的物理器件提供基础。从2017年以来,高阶拓扑绝缘体和高阶拓扑半金属,作为一类全新的拓扑相,相继被发现和研究,其大大拓展了物质拓扑相家族的种类。相比于传统的拓扑相(一阶拓扑相),高阶拓扑相往往具有更低维度的拓扑边界态,比如在三维高阶拓扑绝缘体中存在的零维拐角态 (corner state) 和一维铰链态 (hinge state),三维高阶拓扑半金属中存在的铰链费米弧(hinge Fermi arc)等。鉴于这一新兴领域的快速发展,本文基于拓扑能带论,对高阶拓扑物理进行了简要的回顾,并重点聚焦于用经典波系统(诸如光子晶体,声子晶体等)实现各种高阶拓扑相。进一步地,对高阶拓扑的未来发展方向进行了展望。
创新研究
高阶拓扑物理的起源
历史上,高阶拓扑绝缘体的发现源自多个方面。一方面,当研究从体哈密顿量衍生出的边界哈密顿量描述的无能隙边缘态的时候,人们发现这些无能隙边缘态可以进一步地被额外的对称破缺项给破坏,从而产生边界哈密顿量的拓扑相变。另一方面,人们发现过去用来描述传统拓扑相的拓扑不变量都具有类似偶极子积分形式。一个自然的问题是:是否存在由更高极距(诸如四极子和八极子)积分形式刻画的拓扑不变量和拓扑相呢?答案是肯定的,这导致了量化多极子绝缘体的诞生。此外,传统拓扑绝缘体的边界态仅仅比体态低一个维度,而实空间拓扑缺陷态可以比体态低更多维度,这种实空间拓扑缺陷态是否是由体拓扑相决定?对这个方向的研究启发了泛高维SSH模型(generalized higher-dimensional SSH model)中高阶拓扑相的发现。在考虑局域带隙中的格林函数的零本征值问题时,人们也发现低维拓扑边界态可以作为高余维(higher-codimensional)杂质束缚态(impurity-bound state)出现。尽管这些工作在某种程度上发现了高阶拓扑相,高阶拓扑绝缘体这一概念直到2017年才被清晰的提出和讨论。自此以后,高阶拓扑物理这一领域迎来的爆发式的发展,吸引了广泛的注意。
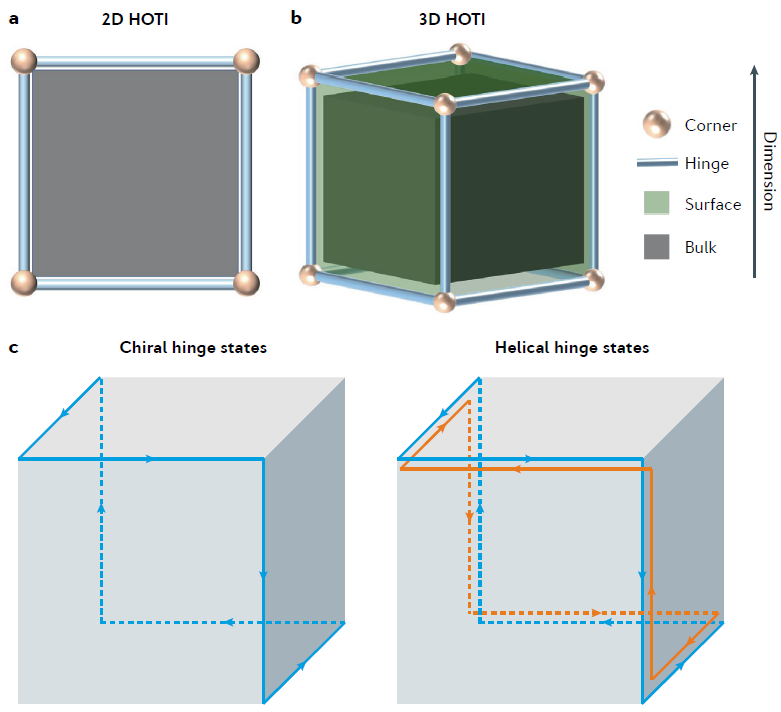
图-1. 具有多维度拓扑边界态的高阶拓扑绝缘体
量化多极子绝缘体(quantized multipole insulators, QMIs)
作为第一类被发现的高阶拓扑绝缘体,QMIs 被定义为具有零体偶极矩且具有量化的体四极矩或者更高极矩的的绝缘体。其可以用具有负耦合的最近邻耦合紧束缚模型实现。由于其特殊性,QMIs 往往需要至少两条能带和非对易的对称性(紧束缚模型中的负耦合)。
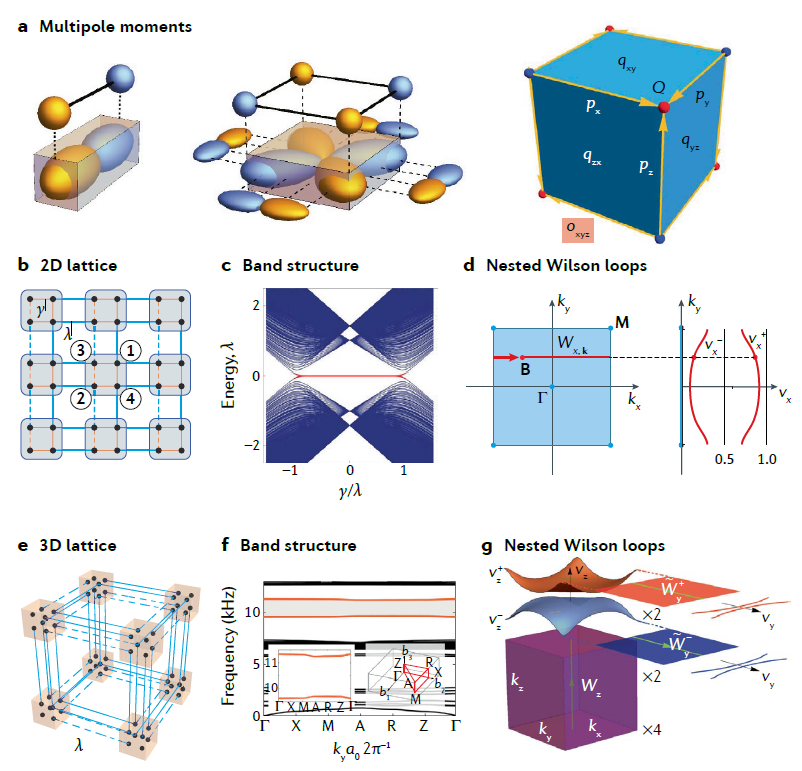
图-2. 量化多极子拓扑绝缘体及Nested Wilson loop。
泛高维SSH模型
与QMIs 不同,高阶拓扑也可以通过将简单的一维SSH模型推广到更高维度和更多样的旋转对称性实现。最简单的例子便是二维SSH 模型。其中存在的零维拐角态是由于拓扑晶体绝缘体中,拐角结构切到了实空间Wannier center导致的。拐角态具有的分数化特征,是由于填充反常:本征模式数和体系旋转对称性不匹配导致的。
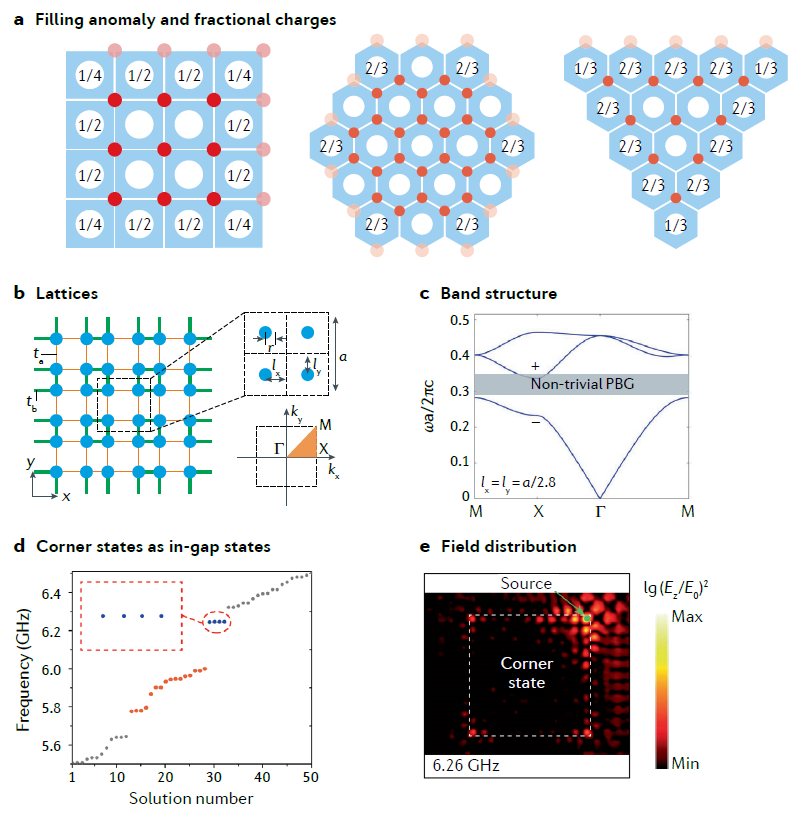
图-3. 二维SSH模型中填充反常诱导的具有分数化特征的拐角态
经典波系统作为探索高阶拓扑相的优良平台
由于高阶拓扑相往往存在于具有特殊晶体空间群对称性的系统,或者需要系统具有负耦合,因此经典波系统,诸如光子晶体、声子晶体、电路系统等是实现高阶拓扑相的良好平台。同时高阶拓扑相所具有的独特的物理效应,比如多维度边界态和分数化荷等,又为实现具有特殊功能的光、声、电器件提供物理基础。

图-4.多种实现了高阶拓扑相的经典波平台。
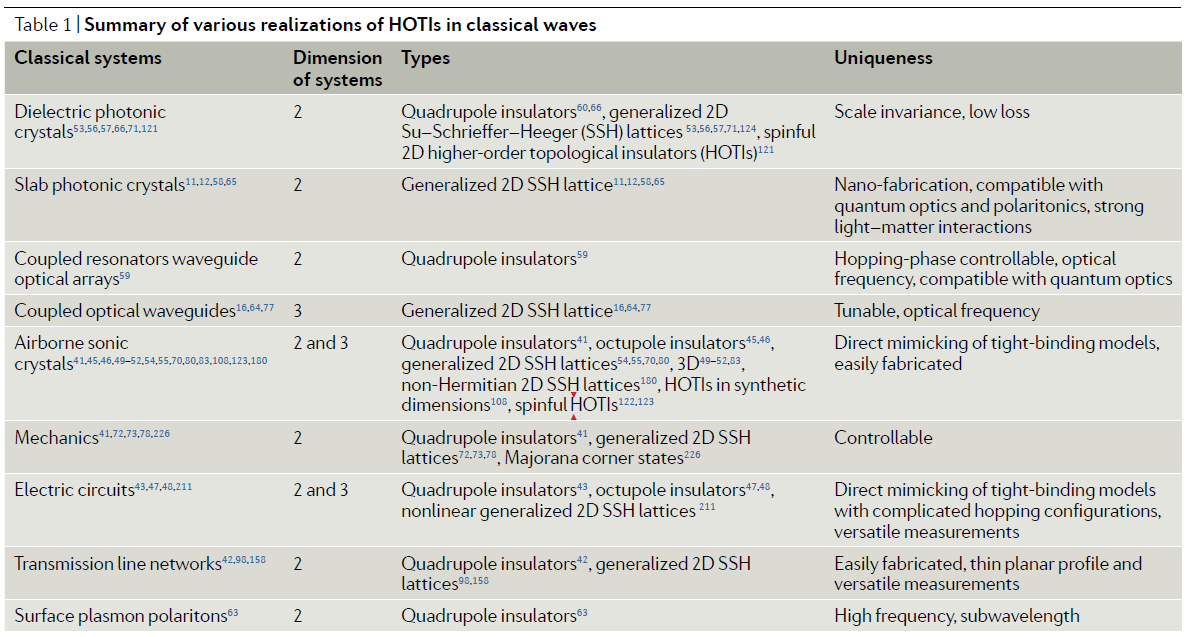
表-1.不同经典波系统实现高阶拓扑相的优势。
未来展望
高阶拓扑物质相作为一个诞生仅四年的领域,目前仍然面临着许多未知的问题,亟待人们的深入探索。比如分数化的电荷、多维度体边对应关系、拐角态作为任意子的非阿贝尔编织,合成维度的高阶拓扑等。另一方面,高阶拓扑相也可以与其他领域结合带来诸多新奇的物理效应,比如与含时Floquet系统、非线性、非厄米、量子光学、无序结构、超材料等领域。最后,高阶拓扑相也为设计具有颠覆性功能的器件提供可能。比如实现具有多维度的拓扑激光、高Q值的腔、可重构器件等。
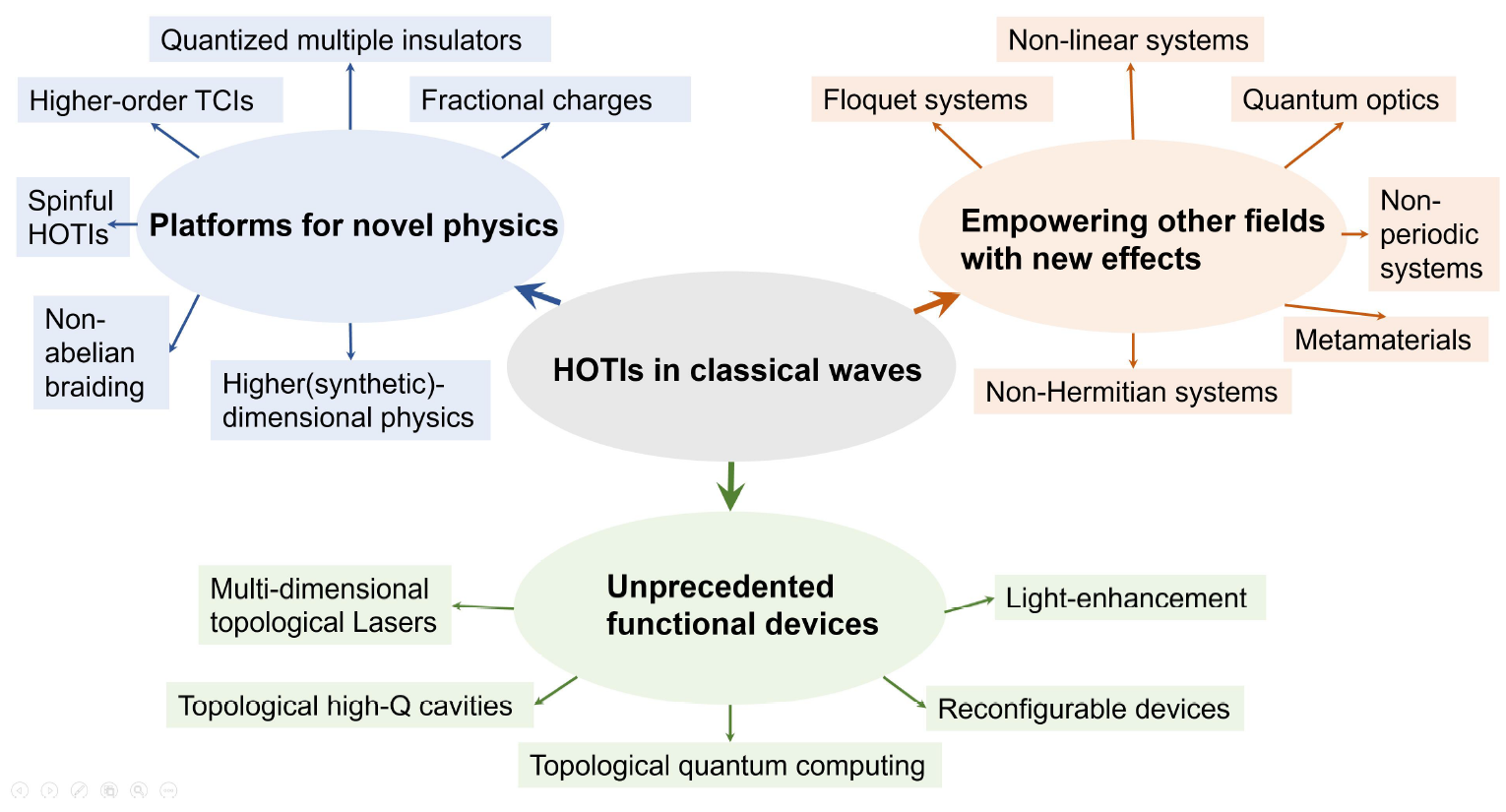
图-5. 经典波中的高阶拓扑带来的新物理研究平台,与其他领域结合带来的新效应和具有前所未有的新功能器件。
(来源“两江科技评论”公众号)


